最近,Noldus 再次对动物步态分析系统(CatWalk XT)进行了创新。最新升级的 CatWalk XT 10.7进行了许多改进,让我们一起来看看吧!
Phase dispersions和Coupling
10.7 中更新的主要内容之一是Phase dispersions和Coupling参数的可视化和计算方式。尽管旧方法并没有错误,但我们发现以前表示这些参数的方式并不直观,可能会导致对参数值的错误解释。由于Phase dispersions和Coupling是最难掌握的两个参数,而且这需要对Circular statistics有一些基本的了解,我们将在本文中对这些概念进行更多的介绍。
步态分析基础:步态周期
在开始之前,我们先来回顾一下步态周期的不同部分。步态周期是指动物行走时脚掌的重复运动。当啮齿类动物的脚跟接触地面时(定义为初始接触)开始,同一脚跟再次接触地面时结束。步态周期可分为两个阶段:
站立阶段:爪子接触地面
摆动阶段:爪子在空中移动
啮齿类动物是四足动物,因此有四只爪子,它们通常以略微不同的偏移量相互循环。如下图所示,偏移量是每只爪子步态周期开始的时间,数字之间的时间距离就是偏移量。
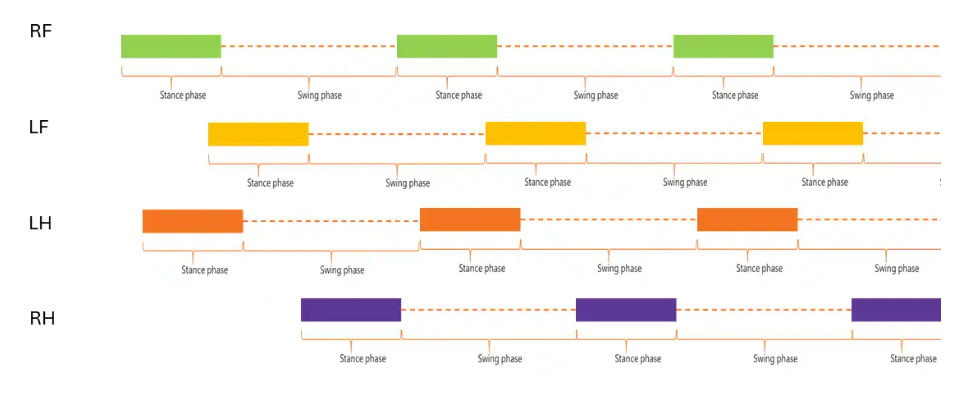
站立阶段又可分为两个阶段:
制动阶段:从初始接触开始,到爪子完全平放在地面上(最大接触)时结束。
推进阶段:从最大接触后开始,到爪子完全离开地面时结束。
由于啮齿动物是四足动物,因此有 24 种潜在的脚步顺序。然而,在剔除镜像和重复模式后,只剩下三种截然不同的模式。这些模式的时间以及两个不同脚爪步态之间的距离对于测量Phase dispersions和Coupling至关重要。
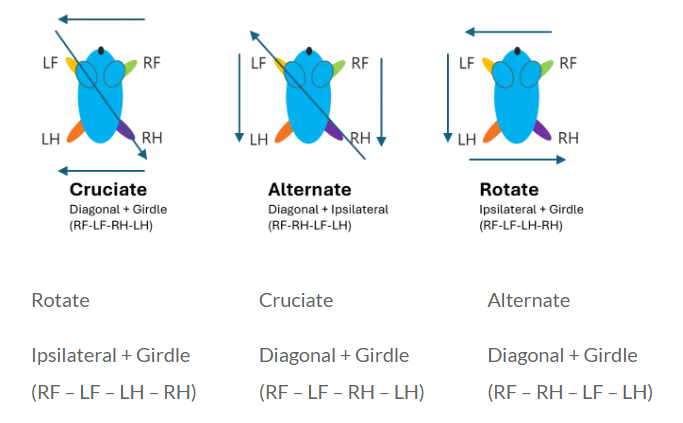
解释Phase Dispersions和Coupling
我们试图用Phase dispersions和Coupling参数来研究的是一对爪子之间的偏移。换句话说,在一只爪子("锚")的步态周期中,另一只爪子("目标")的步态周期从哪里开始。测量值是偏移量占锚点步态周期的百分比。这两个参数之间的区别表述如下:
l Coupling侧重于两只爪子之间的关系及其相互协调。由于其定义,Coupling度总是在 0-100% 的范围内
l Phase dispersions侧重于步态周期之间的时间和一致性的可变性
举例来说,当右前爪的步态周期总持续时间为 20 毫秒并被视为锚点时,左后爪的步态周期在锚点开始后 15 毫秒开始。这就意味着左后爪在锚点步态周期的 75% 时触地。Coupling参数和Phase dispersions的值均为 75%。
在步态分析中使用Circular Statistics
由于基础数据具有重复性,因此我们需要使用Circular statistics来计算一次运行、一次试验或一组动物中一组数值的平均Phase dispersions。让我们举一个简化的例子,数据来自四个步态周期:两次为75%,两次为5%。线性统计得出的平均值为40% [(75+75+5+5)/4],但这是不正确的。
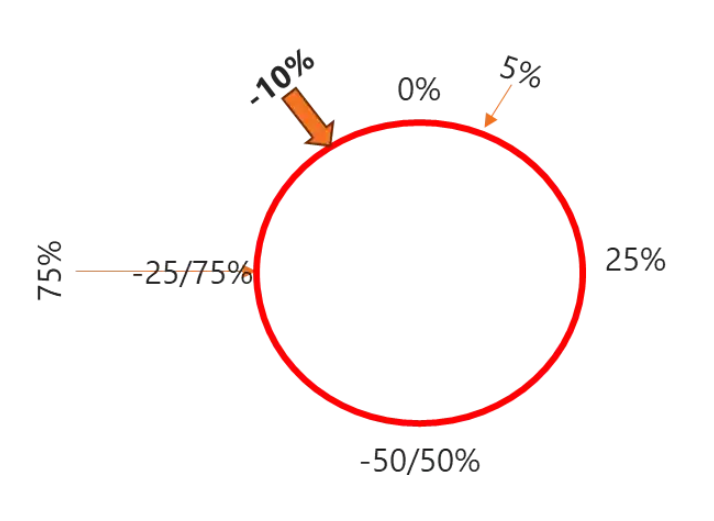
在Circular statistics中,数据点被绘制在一个圆圈上。对于Phase dispersions,圆的顶部为 0%(和 100%),顺时针方向移动,右侧为正值25%,底部为50%,左侧为75%。逆时针方向则为负值。因此,像75% 和-25% 这样的值在这个圆上是同一个点。
以刚才提到的例子为例,当我们在圆圈上画出5%和75%时,它们在逆时针方向上靠得更近,使得平均值为-10%(或90%),而不是40%。这个例子中的值是-10% 还是90%,取决于参数的定义。Coupling度范围为0%-100%,Phase dispersions范围为-50%至75%。
因此,Phase dispersions的值为-10%,而Coupling度则为90%。这说明了对该参数进行循环分析的必要性,以及我们引入循环分析以避免解释错误的原因。
联系我们了解更多信息!
您是否还需要了解更多有关Phase dispersions、Coupling或动物步态分析系统(CatWalk XT)的信息?填写下方表单联系我们了解更多信息!
关注诺达思公众号,联系我们获取更多产品信息及学术文章!

